Circles In Geometry | A Basic Guide
From ancient times circles have been considered the purest shape there is. Let’s take a look at some of the basics of circles.

From ancient times circles have been considered the purest shape there is. This is likely because celestial bodies, such as planets and moons, which were associated with the gods, appeared circular to the naked eye. But beyond the cultural significance, circles possess wonderful properties and traits that have helped to shape our understanding of geometry, trigonometry, complex numbers, and other mathematical concepts. Let’s take a look at some of the basics of circles.
Definition of a circle
Although circles are visually a very simple shape, many students struggle to define what a circle really is. A circle can be defined as the path in which a point moves such that it is always at a constant distance “r” away from point O. In this case, “r” is the radius and O is the center of the circle.
Construction of a circle
Constructing a circle by hand requires a compass, which can be used by adjusting the distance between the legs to the desired radius, placing the tip of one leg at the center, and rotating a full turn around the center.
However, if the exact center is unknown, it’s essential to have at least three distinct points on the circle. This is because a minimum of three distinct points on the circumference is required to define a unique circle in 2D space.
To construct a circle in such a scenario, follow these steps:
Step 1: Connect the points to form a triangle.
Step 2: Draw two perpendicular bisectors on any two sides of the triangle.
Step 3: The point of intersection of the perpendicular bisectors will be the center of the circle that passes through all three vertices of the triangle.
Step 4: Use a compass and adjust the legs from the center to any given point. Then, complete the circle.

The above construction is also known as the circumcircle of a triangle. Note that it is essential that the 3 points are distinct and are not in a straight line.
Features of a circle
There are various features that are useful in describing various geometrical properties of circles. Some of the primary components are:
- Radius – The distance from the center to any point on the circle.
- Chord – A line joining two points on a circle.
- Diameter – The distance of the line passing from one point on the circle to another through the center of the circle. The diameter is the longest chord of any given circle and is twice the size of the radius.
- Arc – A section of the circumference in a circle is known as an arc.
- Circumference – The perimeter of a circle
- Sector – A region enclosed by two radii and an arc is known as a sector.
- Segment – A region enclosed by a chord and an arc.
- Tangent – A line drawn to touch a circle at a single point

Pi and the Circle
Pi is the most famous constant in mathematics derived from the study of circles. It is used widely in various fields of study, such as geometry, algebra, and complex numbers. The irrational number pi was derived from the study of circles. Ancient mathematicians understood that the diameter of a circle was proportional to the size (circumference) of a circle, yet determining the exact ratio was a challenge in geometry. Pi is the ratio between a circle’s circumference and its diameter, i.e. Circumference/Diameter = pi.

Area of a circle
Unlike polygons, determining the space occupied by a circle was not straightforward for ancient mathematicians. Thanks to the contributions from mathematicians like Archimedes and Heron of Alexandria we now know that the area of the circle can be calculated using the formula A = pi*r^2
Simple Proof for Area of a Circle
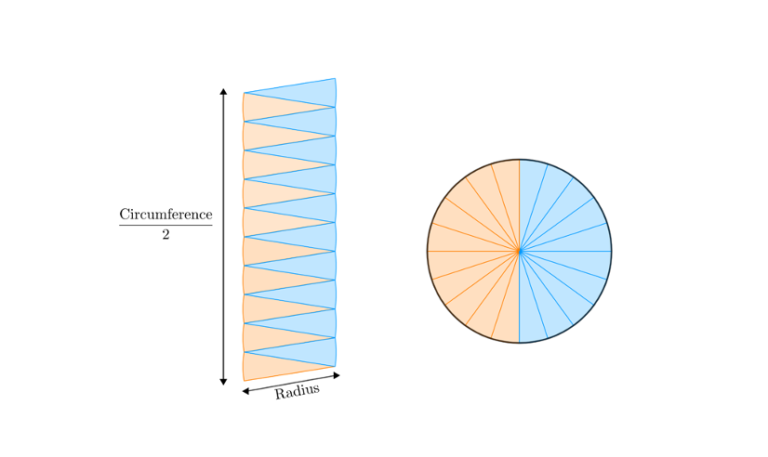
To gain a better understanding of why the formula works, we can use a visual approach.
We can picture a circle being divided into sectors and arranged in a row. This arrangement creates a rectangle of length pi*r and the height of the radius itself. This rectangle provides a convenient way to calculate the area of the circle. By multiplying the length and width of the rectangle we get the formula for the area of a circle.
Arc length of sectors
The arc length is a portion of the circumference of a circle, and it is proportional to the central angle. For example, for a semi-circle, the arc length would be half of the circumference, as the central angle is 180 degrees (half of a full circle 360 degrees).
A generalized formula that can be used to determine the arc length of the sector can be given as:
(θ/360) x Circumference. Here, θ represents the central angle of the sector. Determining the arc length is crucial in calculations concerning circular paths or constructions. In fact, the earliest calculations of the size of the Earth (Diameter and circumference) were done using this concept. Over 200 years ago, the Greek mathematician Eratosthenes calculated the distance between two cities (the arc length) and obtained the central angle of the arc to derive an estimation for the full circumference of the circle, and in turn the diameter of the Earth.

Area of sectors
A sector is a part of a whole circle. If we know what fraction of the circle the sector covers then it is possible to calculate the area using the following formula:
Area of sector = fraction of circle * Area of the whole circle
We often use the central angle to determine the fraction of the circle covered by the sector. For example, if the central angle of a sector is 45 degrees, the fraction would be 45/360. The formula used above can be generalized as:
The central angle of sector/360 * π * r ^2
Conclusion
Circles are not only interesting shapes but also fundamental in many areas of mathematics and science. From basic geometry to advanced calculus, circles play a key role in numerous fields. The properties of circles, such as their radii, diameters, chords, and tangents, are essential to understanding their behavior and applications.
ip between the sizes of the three sides in a right triangle. There are widespread use cases of the Pythagorean theorem in fields like engineering, architecture, physics, etc. The 3-4-5 method and the shortest distance calculation are examples of techniques based on the Pythagoras theorem that can be beneficial for everyone to apply in real-life situations.