How To Find The Volume Of Cones | A Basic Guide
From the simple traffic cone to the complex rocket nose cone, the cone is an essential component of modern technology and innovation. In this article, we will explore cones and their variants and learn how to determine the volume of cones.

The cone is a geometric solid with wide-ranging applications in various fields, including construction, aerodynamics, and engineering.
The Right Circular Cone
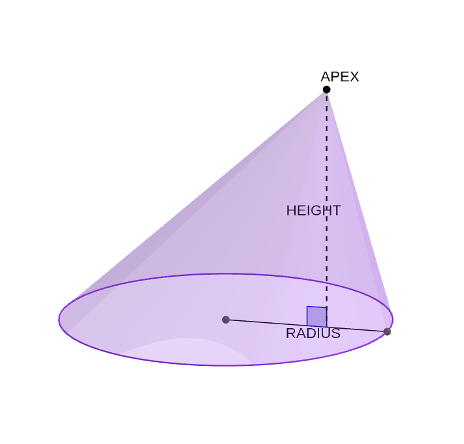
The cone is a three-dimensional shape with a flat base and a curved surface that tapers smoothly to a point (aka, the apex). The features that help distinguish cones are the shape of the base, height, and slant length (distance from the base edge to the apex).
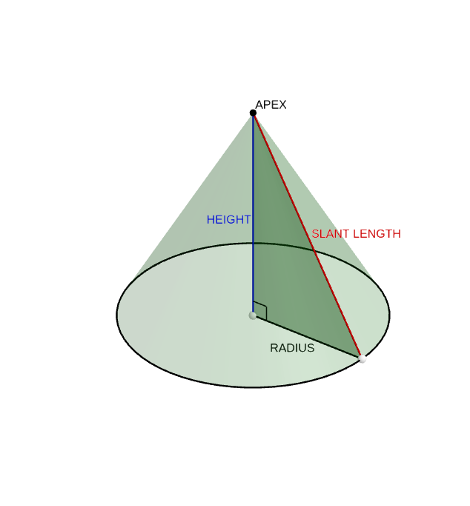
The right circular cone is a type of cone that is extensively studied in geometry. It has a circular base and the line that connects the center of the base with the apex of the cone is perpendicular (at right angle) to the radius of the base.
There are several other variations of the cone such as:
- The elliptical cone has an elliptical base, distinguishing it from a conventional right cone.

- The oblique cone – When the line connecting the apex and center of the base is at an angle other than 90 degrees, it is an oblique cone.
- A truncated cone is a three-dimensional object that has a flat surface at the top instead of a pointed tip. To visualize a truncated cone, imagine slicing a plane parallel to its base at some height of the cone. The original cone will be separated into two parts: a smaller cone at the top, and a truncated cone at the bottom, which has a top surface similar to its base. A coffee cup is a real-life example of a truncated cone.

How To Find The Volume Of A Cone
The formula for the volume of a cone is given by ⅓ pi*r^2*h, where r is the radius of the base and h is the perpendicular height from the base to the apex. However, deriving the volume of a cone can be challenging as the cross-section along the height is not uniform, unlike objects such as cylinders or cuboids.
Despite this, a right circular cone shares several characteristics with other 3D objects with curved surfaces, such as cylinders and spheres. In terms of volume, a cone is one-third that of a cylinder with the same base radius and height. Since, the volume of a cylinder like any prism is Cross-section area * height, which is pi*r^2*h the formula for the cone above becomes intuitive.
Example #1: Determine the volume of a right circular cone with a diameter of 6m and a height of 10m.
Step 1: Identify the measures of the cone
In this example, the diameter of the cone is given as 6 meters. To find the radius, we divide the diameter by 2. Therefore, the radius (r) is 6 m / 2 = 3 m. The height (h) of the cone is given as 10 meters.
Step 2: Apply the formula
The volume (V) of a right circular cone can be calculated using the formula:
V = 1/3 π r^2 h
r is the radius of the base of the cone
h is the height of the cone
Substituting the known values:
V = 1/3 × π × (3^2) × 10
V = π × 30
V ≈ 94.2 cubic meters
The Volume Of A Truncated Cone
To find the volume of a truncated cone, you can use the height of the cone before it was cut. First, calculate the volume of the larger cone that the truncated cone was originally a part of. After that, subtract the volume of the smaller cone that was cut off from the top. The result will be the volume of the truncated cone.
A more straightforward approach is to apply the formula Volume = ⅓*pi*r^2*h*(r² + r * R + R²), where, ‘r’ and ‘R’ are the base radii, such that R > r, and ‘h’ is the height of the truncated cone. This formula allows you to find the volume of a truncated cone directly, without the need for any additional calculations.
Calculating the Volume of a Cone: Alternative Methods
In certain scenarios, the necessary dimensions for calculating the volume of a cone might not be directly available. For instance, you might have the slant length instead of the height, which prevents the direct application of the standard cone volume formula. However, in a right circular cone, the radius, height, and slant length form a right triangle. This means that you can use trigonometry and the Pythagorean theorem to determine the missing measurements and calculate the cone’s volume accurately.
- slant length (l) and radius (r) : Using Pythagorean theorem -> h = sqrt(l2 – r2)
- When only the slant length and height are available: Using Pythagorean theorem -> r = sqrt(l2 – h2)
- When the slant length and the angle at the apex are given: Using trigonometry -> h = l*Cos(angle) and r = l*Sin(angle)
- When only the angle at the apex and height are known: Using trigonometry -> r = h*Tan(angle)
- When only the angle at the apex and radius are available: Using trigonometry -> h = r/Tan(angle)
Conclusion
The cone is a fundamental shape with a range of applications in various fields, from construction to aerodynamics. There are various types of cones and different measures used to describe a cone. Whether you’re a student, engineer, or just interested in the geometry of the natural world, this article will help you learn the skills of working out the volume of the right circular cones and other variants.