What Are Angles In Geometry? Types and Examples
Angles are a core component of geometry. In this article, let’s explore what angles are and the different classifications of angles that you are likely to come across when learning geometry.
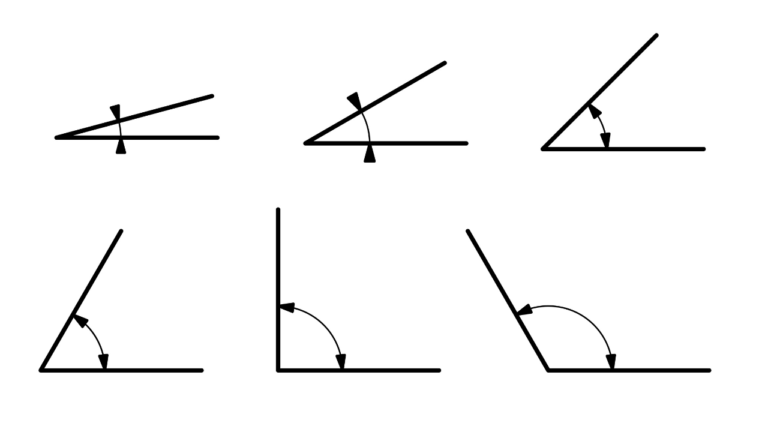
Angles are a core component of geometry. Angles help construct and describe geometric objects accurately. An angle is always based on perspective and is used to communicate the direction in geometry. In this article, let’s explore what angles are and the different classifications of angles that you are likely to come across when learning geometry.
What is an angle?
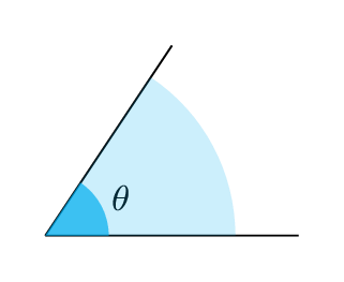
An angle serves as a measure of the space between two intersecting lines. Angles are crucial for describing rotations or orientation of geometrical objects. There are primarily two units for measuring the angles, degrees, and radians.
Degrees and Radians
The usage of degrees as a measuring unit for angles dates back to the Babylonian period. In this system, a full circle is divided into 360 degrees. Why 360? 360 is a highly composite number as it has many factors, which makes it versatile for dividing circles into equal parts. Consider the simplicity of dividing a circle into thirds in this system – each sector forms a neat 120-degree angle. Now, imagine using 100 degrees as a full circle, dividing it into thirds would result in a less intuitive 33.333… degrees for each sector. The 360-degree system simplifies such calculations, making it a longstanding choice in geometry.
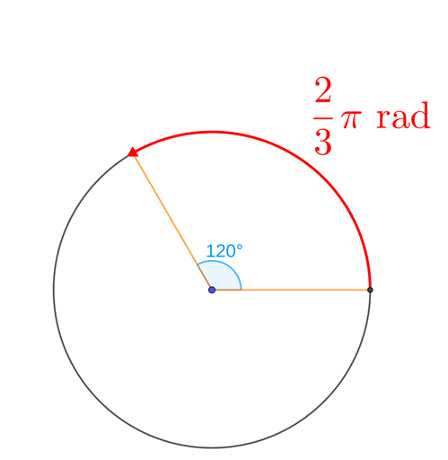
Radians, a more nuanced unit, measure angles based on the arc length of a unit circle (a circle with a radius of 1 unit). Here, a full rotation corresponds to 2pi radians, directly linked to the circumference of a unit circle, which is 2pi. As the angle is always proportional to the arc length if the ratio of a given angle to a full rotation is known, the angle measure can be calculated in radians. For instance, an angle that spans a third of a circle is 2π/3 radians, since it’s a third of the full 2π rotation.
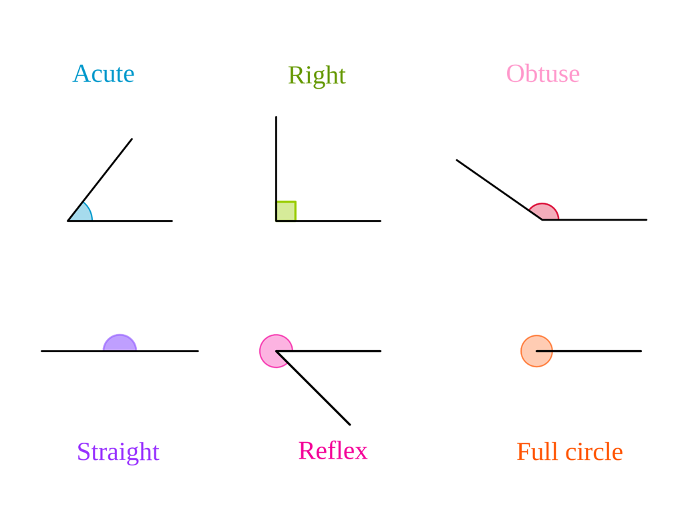
Acute Angles
Angles less than 90 degrees are known as acute angles. Picture the rotation of a door in your home – it often swings through an acute angle. Visually an acute angle is depicted by an arc sweeping less than a quarter of a complete circle.
Geometrical objects like triangles, parallelograms, and trapeziums are composed of at least one corner which is an acute angle. Acute triangles get their name because they are triangles made from 3 corners that have acute angles.
Right Angles
Right angles are angles of size 90 degrees. They are formed at the intersection of perpendicular lines. They are foundational elements in various mathematical disciplines, including vector analysis, transformations, and trigonometry. While other angles are often represented by arcs, the right angle is conventionally indicated by a square. The Pythagoras theorem pivots around right triangles, which are triangles with a right angle.
A shape with all corners being right angles is known as a rectangle. The square is a special type of rectangle.
Right angles are integral to our daily lives as well. Whether it’s meticulously building shelves and desks to align perfectly with a wall or vertical surface, or ensuring balance and stability of structures, right angles are important.
Obtuse Angles
Angles of size greater than 90 but less than 180 degrees are classified as obtuse. All regular polygons with more than 4 sides are composed of obtuse angles at each interior corner. Obtuse angles are represented using arcs spanning between a quarter and a semi-circular arc.
Straight Angles
A straight angle is precisely what its name suggests – an angle formed at a straight line. You can also imagine this as the angle formed in a half-turn. The arc used to indicate a straight angle is a semi-circle. In vectors, two vectors that are in directly opposite directions form a straight angle at the intersection.
Reflex Angles
An angle greater than 180 degrees and less than 360 is known as a reflex angle. Reflex angles are less commonly encountered in basic geometry compared to acute, obtuse, and straight angles, but they are crucial in advanced geometric concepts and calculations.
Properties of angles
In geometry, we discuss relationships of angles in pairs. These relationships are useful for determining congruency and similar shapes. Examples include complementary, supplementary, corresponding, alternate, and vertically opposite angles.
These angle relationships are not just theoretical; they have practical applications in real-world scenarios. For instance, devices like clinometers that measure angles of elevation or depression leverage these relationships to measure heights and distances.
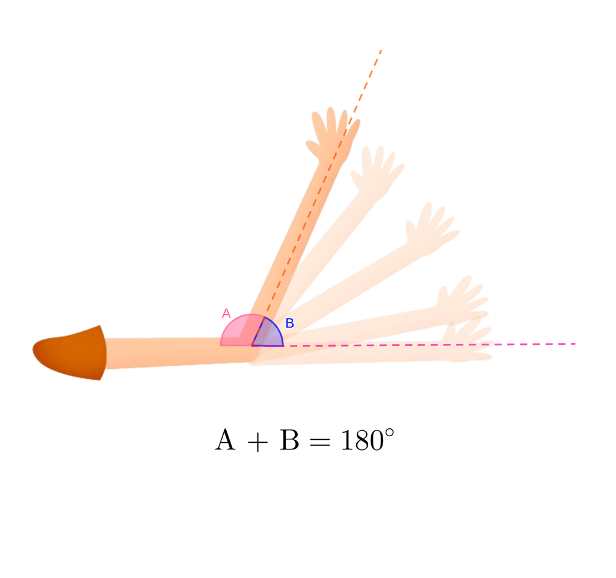
Supplementary Angles
Supplementary angles are pairs of angles whose sum is 180 degrees. Every acute angle has an obtuse angle as its supplementary. For example, if we have an angle of 60 degrees, its supplementary partner is 180 – 60, which equals 120 degrees. A familiar real-life example of supplementary angles is the bending of your arm at the elbow. The angle formed by your bent arm, combined with the additional angle through which it can still bend, forms a supplementary pair. The concept is illustrated below.
Complementary Angles
If the sum of two angles is 90 degrees they are known to be complementary angles. Complementary angles are always a pair of acute angles. For example, 30 degrees and 60 degrees are a pair of complementary angles. Another way to visualize complementary angles is by bisecting a, resulting in two angles of 45 degrees each.
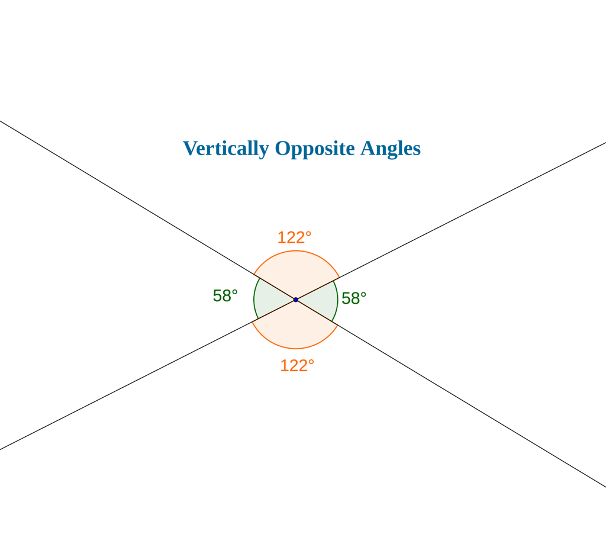
Vertically Opposite Angles
At the intersection of two non-parallel lines two pairs of congruent angles are formed directly opposite each other. These pairs are known as vertically opposite angles. Vertically opposite angles can vary in size; they can be either acute, obtuse or even right angles, depending on the inclination of the intersecting lines.