How Is The Pythagorean Theorem Used In Geometry?
The Pythagorean theorem is widely regarded as the most famous principle in geometry. In this context, let’s delve into what the theorem is and how it is used in geometry.
Pythagoras Theorem
The Pythagorean theorem explains the relationship between the lengths of the three sides of a right triangle. A right triangle is a triangle that has one 90-degree angle.
The Pythagorean theorem states that the square of the longest side of a right triangle is equal to the sum of the squares of the other two sides. This is represented mathematically as a^2 + b^2 = c^2.
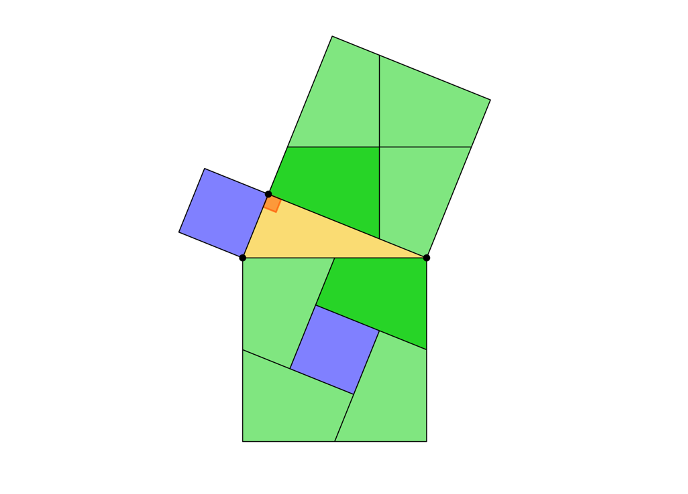
Another way to visualize this concept is by looking at the squares placed on each side of the right triangle. The length of each square is equal to the length of the corresponding side of the triangle. The Pythagorean theorem tells us that the area of the square on the hypotenuse (the longest side) is equal to the sum of the areas of the other two squares. It’s interesting to note that this theorem is not only true for squares but also for semicircles, triangles, and other shapes.
Finding missing sides
Pythagoras theorem can be used to find the length of sides of right triangles. To apply the theorem, the length of two sides must be known. For instance, consider the following example: if the longest side (hypotenuse) length is unknown, but the other two sides are known, we can apply the Pythagoras theorem. By doing so, we can determine the length of the hypotenuse. In the example below, the two sides have lengths of 3m and 4m respectively. Applying the Pythagoras theorem, we get c^2 = 3^2 + 4^2 which simplifies to c^2 = 25. Therefore, c is equal to the square root of 25, which is 5m. Thus, we have determined that the hypotenuse is 5m in length.
Determining the area of triangles
To calculate the area of a triangle, we use the formula ½*base*height, where the height is always perpendicular to the vertex from the base. If the perpendicular height is unknown, we can use Pythagoras’ theorem.
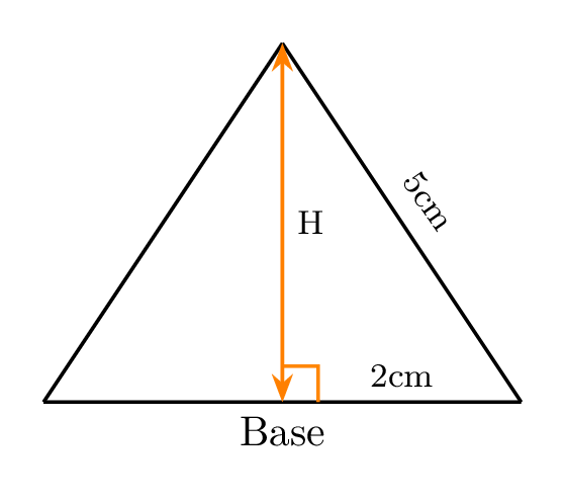
For instance, consider the following example:
In this case, since the height is perpendicular, triangle ABD is a right triangle, and the Pythagorean theorem applies. We can apply the theorem as follows: 5^2 = 2^2 + H^2 and solve for H to get H = ~4.58cm. It’s important to note that the choice of sides a and b is not significant, and they can be alternated. However, c is always the longest side of the right triangle, which is also known as the hypotenuse.
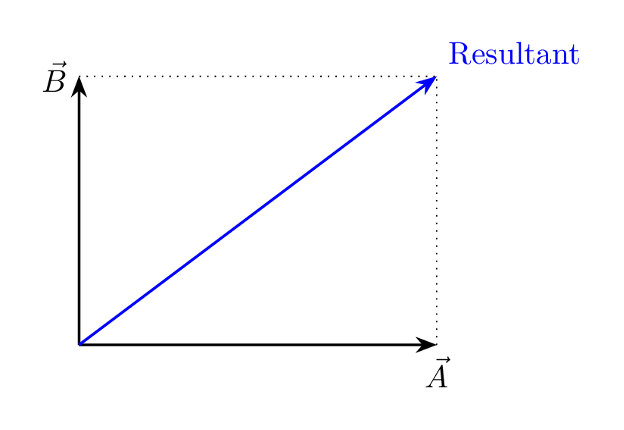
Magnitude of Resultant
Pythagoras’ theorem is an essential tool when dealing with vectors in physics. To evaluate the resultant force under a system of forces we can first condense all forces into components in perpendicular directions, usually horizontal and vertical. Then we can use the Pythagorean theorem to determine the size of the resultant. For example, consider two forces acting on an object, as shown in the diagram below. According to the vector addition rule the hypotenuse is equal to the magnitude of the two perpendicular forces.
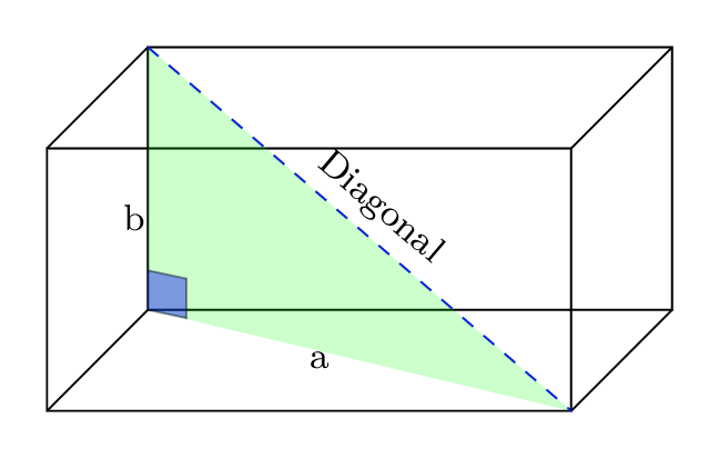
The diagonal of a 3d objects
For 3d objects like cubes and cuboids, the Pythagoras theorem is useful for calculating the diagonal length. In the following cuboid, the diagonal exists in a different plane to the front face, which can be challenging at first. Nevertheless, you can still apply the Pythagorean theorem by selecting the appropriate right angle in which the diagonal is the hypotenuse.
The square root operation
Did you know it is possible to draw line segments of size that are irrational? With just a ruler, it’s impossible. Pythagoras’ theorem allows us to geometrically represent irrational numbers like square root (2), and square root (3) as line segments.
The diagram above shows a series of right triangles. The first triangle has side lengths of 1 unit each, which gives us a hypotenuse of side length square root (2) according to the Pythagoras theorem. This can be extended further as a series to obtain the square root of any positive integer.
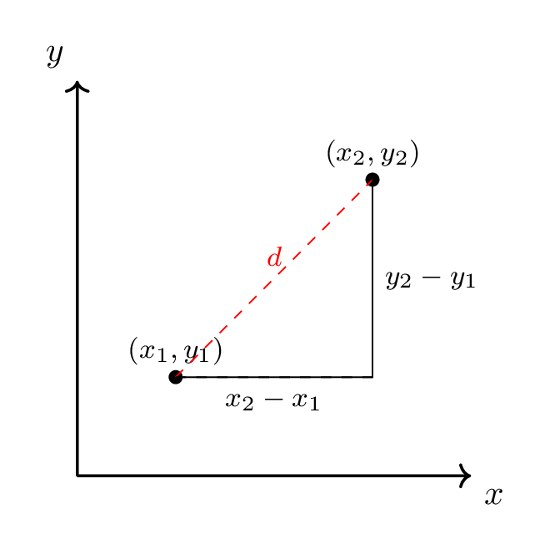
Euclidean distance
Did you know that Pythagoras’ theorem can be used to measure the distance between two coordinates on a cartesian plane? Let’s say we have two points (x1,y1) and (x2,y2). The horizontal distance between the two coordinates is calculated as x2 – x1. Similarly, the vertical distance is calculated as y2 – y1, as shown in the diagram below. To obtain the straight line distance between the two points, we can use Pythagoras theorem and find the length. In coordinate geometry, the formula to calculate the Euclidean distance is the square root of ((x2 – x1)^2 + (y2 – y1)^2), which is derived from Pythagoras theorem.
Shortest distance
In two-dimensional navigation, we can use Pythagoras’ theorem to determine the shortest distance to a desired location. For instance, if you are on a ship traveling to a location that is 300km North and 400km West, you can use the theorem to find the distance from the ship to the location as follows: 3002 + 4002 = c2, c = 500 km. Thus, the shortest distance to the location from where you are would be 500 km.
3 - 4 - 5 method
The 3-4-5 method is a surveying technique that helps to obtain square angles easily. The numbers 3-4-5 are known as Pythagorean triples because when they are considered side lengths of a triangle, they satisfy the Pythagorean theorem. Some other triples include 6-8-10, and 5-12-13, etc. This method is useful when you need to create a perfectly square corner, for fencing or decking. To do this, a rope is used to form a triangle with sides in a ratio of 3:4:5. This technique makes use of the idea that the Pythagoras theorem works for right triangles, and so if the Pythagorean theorem works then it is possible to create a right angle or square corner effortlessly.
Conclusion
The Pythagoras theorem states the relationship between the sizes of the three sides in a right triangle. There are widespread use cases of the Pythagorean theorem in fields like engineering, architecture, physics, etc. The 3-4-5 method and the shortest distance calculation are examples of techniques based on the Pythagoras theorem that can be beneficial for everyone to apply in real-life situations.