How To Solve A Two-Column Proof In Geometry | The Complete Guide
Learning geometry involves applying knowledge to verify or prove various properties of geometric shapes. In this article, we will explore how to apply this method with examples.

Learning geometry involves applying knowledge to verify or prove various properties of geometric shapes. To ensure consistency and methodological accuracy, there are many ways of doing this, one of which is the Two-Column Proof. This systematic approach to geometric proofs provides a step-by-step method for verifying geometric properties. In this article, we will explore how to apply this method with examples.
Understanding Two-Column Proofs
A two-column proof consists of a list of statements, with the corresponding reasons that justify each statement. The left column contains the statements, and the right column contains the reasons. These proofs are like mathematical arguments; they require a foundation of known facts, such as definitions, postulates (assumptions), and previously proven theorems.
The Structure of a Two-Column Proof
- Statement: This column contains every step of the proof, including the given information, the steps you are taking to prove the theorem, and the conclusion.
- Reason: This column justifies each statement. It can include definitions, postulates, properties, or previously proven theorems.

Steps to Solve a Two-Column Proof
- Understand the Problem: Begin by understanding what you need to prove. Read the theorem or statement carefully and understand all the parts.
- Gather Given Information: When approaching a problem, it is crucial to accurately identify and organize all the information provided. This involves creating detailed diagrams, labels, and markings that reflect the given information, as well as constructing any necessary figures that can assist with the proof.
- State What You Need to Prove: Write what you need to demonstrate at the end of the proof.
- Plan Your Approach: Think about the geometric concepts and theorems that might be relevant to the proof. This step might require you to draw a diagram or mark it up to visualize the relationships between different components.
- Write Down the Proof: Start with the given information and logically progress towards the statement you need to prove. Each step should be clear and justified.
- Review and Edit: After writing your proof, review each statement and reason to ensure they follow logically from one another. Ensure that you have stated the desired conclusion at the last line of the statement column.
Example of a Two-Column Proof
Problem: Prove that the opposite angles in a parallelogram are congruent.
Given: Quadrilateral ABCD is a parallelogram.
To Prove: Angle A is congruent to angle C, and angle B is congruent to angle D.
Before applying the column approach, let’s try to add the useful information into the diagram as it will assist our proof process. Below, we have indicated the pair of parallel sides using the arrow notation.
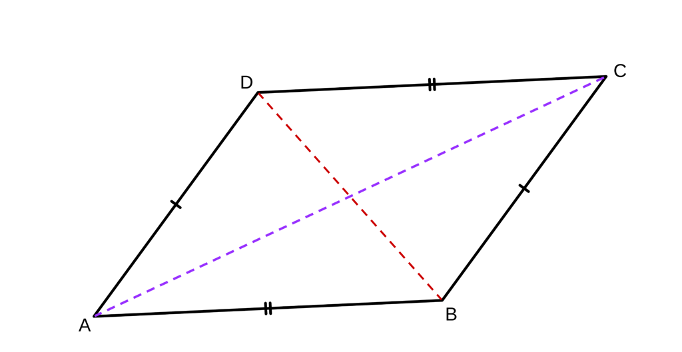
Statements | Reasons |
ABCD is a parallelogram | Given |
AD ≅ BC, and AB ≅ DC. | Definition of a parallelogram |
AC ≅ AC and BD ≅ BD | Reflexive Property |
Triangle ACD ≅ Triangle ABC | SSS congruence |
Angle B ≅ Angle D | Corresponding angles of congruent triangles ACD and ABC are congruent |
Triangle ABD ≅ Triangle BCD | SSS congruence |
Angle A ≅ Angle C | Corresponding angles of congruent triangles ACD and ABC are congruent |
Opposite angles in parallelogram ABCD are congruent. | From statements 4 and 6. |
This proof demonstrates the structure and process of creating a two-column proof. Each step is supported by a reason, ensuring the argument is logical and sequential.
Example #2 of a Two-Column Proof
Problem: Prove that the sum of the interior angles of a triangle is 180 degrees.
Given: Triangle ABC.

To Prove: Angle A + Angle B + Angle C = 180°

Two-Column Proof:
Statement | Reasons |
Draw a triangle ABC. | Given. |
Construct a line DE parallel to BC, passing through point A. | Construction. A line can be drawn parallel to one side of the triangle through a vertex. |
Angle DAB is equal to Angle B. | Alternate interior angles are equal (since DE is parallel to BC and AB is a transversal). |
Angle CAE is equal to Angle C. | Alternate interior angles are equal (since DE is parallel to BC and AC is a transversal). |
Angle DAB + Angle A + Angle CAE = 180°. | The sum of the angles on a straight line (line DE) is 180°. |
Angle B + Angle A + Angle C = 180°. | Substituting Angle DAB with Angle B and Angle CAE with Angle C from Steps 3 and 4. |
Conclusion: We have proven that the sum of the interior angles of Triangle ABC is 180 degrees.
Tips for Writing Two-Column Proofs
- Use Diagrams: Always draw a diagram if one isn’t provided. It helps visualize the problem and plan the proof.
- Familiarize with Theorems and Definitions: Knowing various geometric theorems, postulates, and definitions is crucial. They form the basis of the reasons in your proof.
- Be Logical and Sequential: It’s essential that each statement in your proof follows logically from the one before it. Avoid making assumptions, no matter how obvious they might seem. In geometric proofs, clarity and precision are paramount, so it’s better to explicitly state even the obvious details than to risk making unwarranted leaps in logic.
- Be Concise but Complete: Your statements should be clear and to the point, but also ensure you’ve included all necessary steps.
- Practice Regularly: Like any skill, writing proofs improves with practice. Solve different types of problems to build your skills.
Conclusion
Two-column proofs are an essential component of high school geometry, helping students develop logical reasoning skills. By understanding the structure, following a systematic approach, and practicing regularly, students can master the art of writing two-column proofs. These skills not only aid in academic success but also enhance critical thinking skills valuable in real-life problem-solving scenarios. Remember, each proof is a small journey from the known to the unknown, and with each step, you’re not just proving a theorem, but also sharpening your mind.