What Are Lines In Geometry? Types & Examples
One of the fundamental elements in geometry is lines. Lines are objects that make up crucial building blocks in our understanding of space and time. In this article, let’s look at what the geometrical definition of a line is and the various types of lines.

What is a line?
A point is a zero-dimensional element representing a precise location in space without any length, width, or depth. A line, on the other hand, emerges as an infinite collection of points aligned in a straight path. This is a one-dimensional figure extending indefinitely in both directions. To depict this infinite nature, lines are visually represented with arrows at both ends.
To define a line in space, a minimum of two distinct points are required. An interesting aspect of lines is their uniqueness: if two lines share two or more points in common, they are considered identical.
The line segment
For practical purposes, it is common to refer to a straight path created by joining endpoints as a line, but it is another geometrical object known as a line segment. The key difference between a line and a line segment is that a line segment has a finite length while the line extends infinitely in both directions.
Line segments are crucial for constructing all polygons and other shapes with straight edges. They are also instrumental in visually representing vectors in mathematics and physics.
Parallel lines
One of the properties of a line is its gradient/slope. The slope is the angle that a line forms with a reference line. In cartesian geometry, the x-axis is conventionally used as the reference line when measuring the slope/gradient of a line. When two distinct lines have the same gradient they are known as parallel lines. A key characteristic of parallel lines is that they never intersect; that is, they do not share any common points in space, no matter how far they are extended.
Conversely, if two lines have different slopes, they are not parallel and will intersect at exactly one point. This principle is central in the graphical approach to solving a system of linear equations, where the solution is found at the point of intersection of two or more lines. Therefore, a real solution to a system of linear equations is obtainable if, and only if, the lines represented by these equations are not parallel.
Examples of Parallel lines
The rays from the sun can be considered to be parallel.

Intersecting Lines
Pairs of lines that meet or cross at a certain point are intersecting lines. In a 2d space, intersecting lines are all pairs of lines that are non-parallel. However, this straightforward definition of intersecting lines becomes more complex in higher dimensions, as explored in the subsequent section on skew lines.
Intersecting lines allow the creation of an enclosed region. All polygons and polyhedrons with straight edges are composed of intersecting lines that converge to form vertices of shapes. An important property of two or more intersecting lines is that they are coplanar, meaning they lie within the same plane. Consequently, a collection of lines intersecting at a single point defines a plane.
Examples of intersecting lines
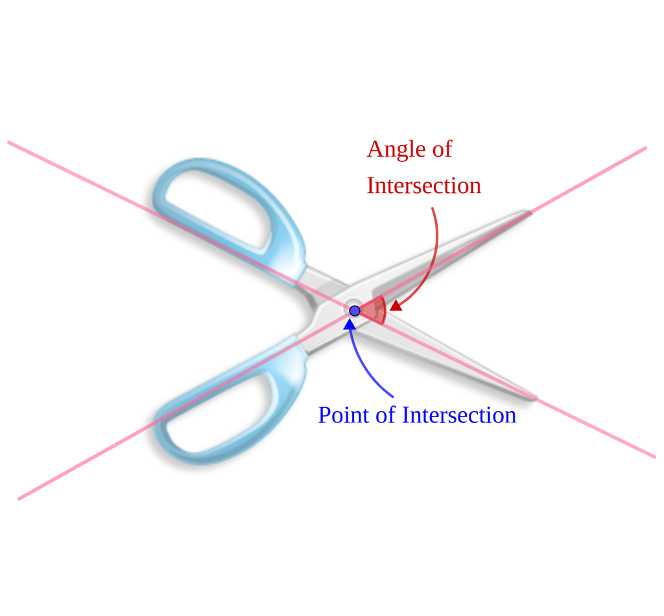
- Scissors and clock hands: A pair of scissors consists of two blades, each represented as a line. The two lines intersect at a pivot or center point. The angle of intersecting changes as the scissors open and close.
- Crossroads: In urban planning, intersecting lines are exemplified by streets and crossroads. Each road can be thought of as a line, and the points where they intersect form the crossroads. These intersections are crucial for directing traffic flow and connectivity in a city layout.
Perpendicular lines
Perpendicular lines are a special case of intersecting lines where the angle of intersection is 90 degrees. The product of the gradients/slopes of two perpendicular lines is always -1. It is a critical principle in geometric proofs and problems used to verify whether a given pair of straight lines is perpendicular to each other.
Examples of Perpendicular lines
- Tangent and Radius: The tangent drawn at a point on the circumference is always perpendicular to the radius that connects the circle’s center to that point.
- Cartesian Coordinates: The x and y axes on a cartesian plane are perpendicular to each intersecting at (0,0) the origin.
- Architectural Elements: The walls and floors of a typical construction are perpendicular. Front sections of floor plan drawings clearly depict the right angles at the intersections.

Skew Lines
In 2-dimensional space, any pair of non-parallel lines will intersect at a single point. However, in 3-dimensions space, it is possible to have non-parallel lines that do not intersect. These lines are called skew lines. To visualize skew lines consider a cube. Imagine two lines on opposing faces as shown below. Despite not being parallel to each other, these lines never meet because they line in separate non-intersecting planes. Note that skew lines do not exist in dimensions below 2D.

Example of Skew Lines
- Pair of Overhead Power Lines: Consider two power lines running overhead, suspended by different poles. As long as the lines are in non-intersecting planes they do not intersect, making them a perfect example for skew lines.
Conclusion
At the heart of geometry are lines, which make up essential building blocks for constructing a wide range of shapes and objects. Understanding the properties of lines is fundamental to mastering geometry, which is why we explore their various types in this article. From the infinite nature of lines to line segments and parallel, intersecting, perpendicular, and skew lines, each type of line has unique properties and applications. Learning about lines is an excellent way to deepen your understanding of geometry and the world around us.