How To Find Surface Area In Geometry
Understanding surface area is very important, especially when dealing with three-dimensional geometric shapes. This article will guide you through the methods of finding the surface area of basic geometric shapes.

Understanding surface area is very important, especially when dealing with three-dimensional geometric shapes. In many fields, such as chip design, heat sinks, packaging, and pharmaceuticals, surface area is a critical parameter that directly impacts the output. Therefore, knowing how to calculate surface area is a key academic skill with practical applications. This article will guide you through the methods of finding the surface area of basic geometric shapes.
What is Surface Area?
To put it simply, the surface area of a three-dimensional object refers to the total area of the object exposed to the surrounding environment. Just imagine painting the exterior of a shape; the amount of paint required to cover it would be directly proportional to its surface area. Unlike two-dimensional shapes that only have area, three-dimensional shapes have both volume and surface area.
Calculating the Surface Area of Common Shapes
3D shapes consist of multiple faces, which can be either flat, curved or a combination of both. Regardless of their type, all these faces contribute to the total surface area of a shape. When calculating the surface area, it is useful to categorize the faces properly and calculate their areas individually, then add them together to obtain the total surface area of the shape.
Let’s look at some step-by-step examples of calculating surface area for common shapes.
Cuboid (Rectangular Prism):
A cuboid has six faces, each a rectangle. To find its surface area, calculate the area of each face and sum them up.

The formula is Surface Area = 2(lw + lh + wh) where l = length, w = width, h = height.
Cube:
Since all faces of a cube are squares of equal size, its surface area is simply six times the area of one face. The formula is Surface Area = 6a^2 where a = side of the cube.
Cylinder:
A cylinder has a curved surface and two circular bases. The area of the flat circular bases can be given as Area = 2πr^2 square units. Curved surfaces are more challenging to work with. It is beneficial to map the net of the cylinder to tackle this. As the illustration shows, the net of the curved surface is a rectangle of height (h) and width equivalent to the circumference of its base.
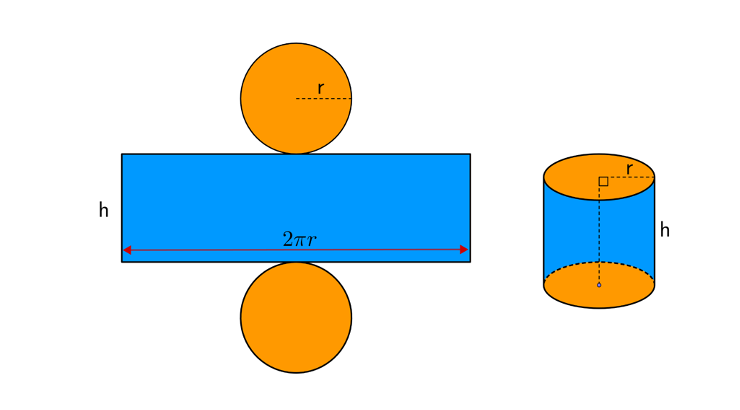
Hence, curved Surface Area = 2πr*h square units. The total surface area is the sum of the area of these parts. The formula is: Surface Area = 2πr(h + r) where r = radius of the base, h = height.
Sphere:
The sphere, being entirely curved, has a surface area calculated by: Surface Area = 4πr^2 where r = radius of the sphere.
Cone:
A cone has a circular base and a curved surface. Like the cylinder, visualizing the net of a cone can be helpful!
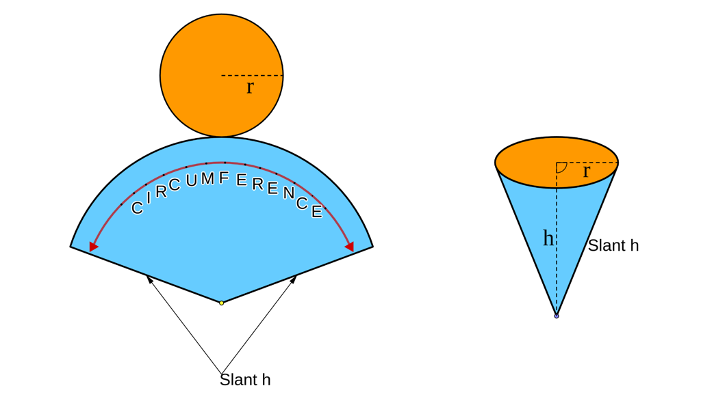
The curved surface, when unrolled, resembles a circular sector with a radius equal to the slant height of the cone, and an arc length that matches the circumference of the base. The surface area includes the area of the base and the curved surface, given by: Surface Area = πr(r + l) where r = radius of the base, l = slant height.
Composite Shape surface area
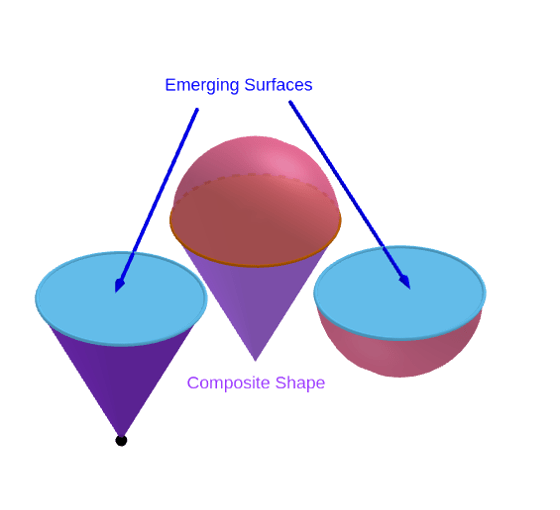
As you advance in geometry, you’ll encounter more complex shapes like pyramids, prisms, and irregular polyhedra. The key to finding the surface area of these shapes is breaking them down into simpler shapes (like triangles, rectangles, etc.), calculating the area of each, and then summing them up. When separating composite shapes into more basic 3D shapes be mindful about the new surfaces that emerge upon separation. These additional surfaces should be excluded from your surface area calculations as they are not part of the exterior of the original shape.
Tips for Finding Surface Area
- Understand the Shape: Familiarize yourself with the shape you are dealing with. Know how many faces it has and what shapes these faces are.
- It’s important to note that recognizing congruent faces or symmetry in shapes can help save time in calculations. This is because it allows you to group them and multiply them instead of calculating each face individually. By using this method, you can simplify the process and make the calculations more efficient.
- Measure Accurately: Ensure that you have the correct measurements for all the dimensions needed for your calculations. Incorrect measurements will lead to the incorrect surface area.
- Consider visualizing the net of an object. A net is essentially a 2D layout that unfolds to form a 3D shape. This technique is beneficial for curved surfaces and intricate 3D objects.
- Memorize Formulas: While understanding concepts is crucial, memorizing the formulas for surface area will save time and help in quick calculations.
- Unit Consistency: Always check that all your measurements are in the same unit. Convert if necessary before starting your calculation.
Real-World Applications
Understanding how to calculate surface area has numerous real-life applications. For example, in architecture and construction, knowing the surface area helps in estimating the material required for building or painting a structure. In packaging and manufacturing, surface area calculations are vital for designing packaging materials. Even in fields like biology or meteorology, calculating surface areas can be crucial for understanding processes like osmosis or heat exchange.
Conclusion
The ability to calculate surface area is not just a key academic skill but also a practical tool. Whether it’s for solving problems in your textbook, designing a project, or just satisfying your curiosity about the world around you, knowing how to find the surface area of various shapes is invaluable. Keep practicing, and soon, these calculations will become second nature to you. Remember, geometry is not just about numbers and formulas; it’s a way of understanding the space and shapes that make up our world.