What Are Transformations In Math? | Types & Examples
Transformations in math are actions that change the position, orientation, or size of shapes. In this article, we will learn more about transformations in math, see different kinds of them, and look at some examples to help us understand them better.

Transformations in math are actions that change the position, orientation, or size of shapes. These actions help us understand and change the shapes we see around us. They also have practical applications in fields like physics, engineering, and computer graphics. In this article, we will learn more about transformations in math, see different kinds of them, and look at some examples to help us understand them better.
Translation
Translation involves moving a geometric object to a different position in space without altering its dimensions or orientation. To define translation in 2-dimensional space we have to specify the desired movement in 2 directions, usually horizontal and vertical. Using a combination of horizontal and vertical movement it is possible to translate a shape to any desired position in space. When dealing with 3-dimensional space, we need to specify movement in three perpendicular directions, x, y, and z.
A 2D translation is represented as a column vector. The first element is the units of horizontal translation, while the second element is the units of vertical translation.
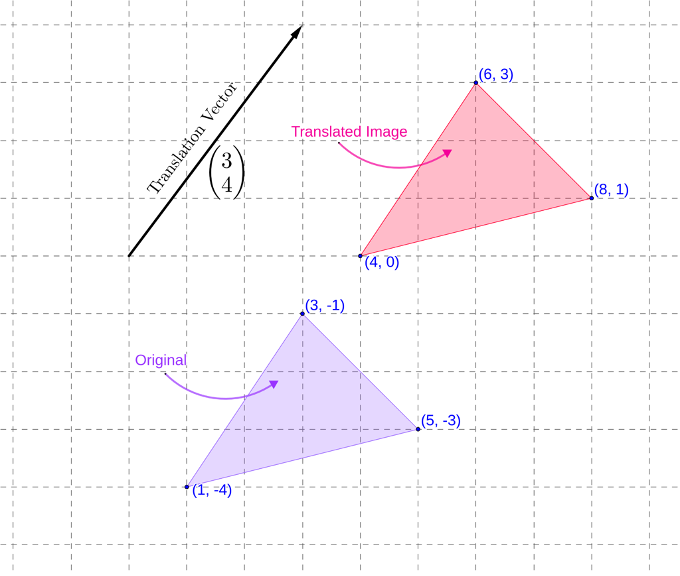
Example: A (4,3) translation vector applied on a triangle is equivalent to moving a triangle 4 units to the right and 3 units up on a Cartesian plane. Every point of the triangle shifts accordingly, but the triangle’s shape and size remain constant.
Rotation
Rotation is a transformation that changes the orientation of a shape while preserving its size and shape. To perform a rotation we need to know the point about which the rotation happens, the degree of rotation, and the sense. The sense of rotation is usually defined as either clockwise or anticlockwise.
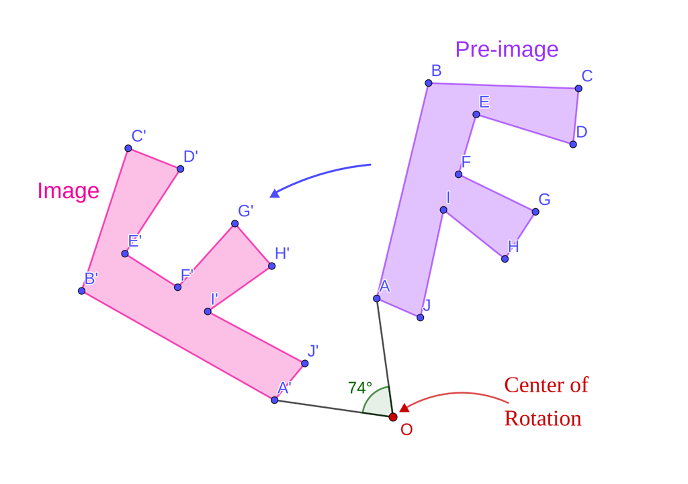
Example: A square rotated 90 degrees around its center will have each vertex move to the position of the next vertex. Despite the rotation, the square maintains its shape and size.
Reflection
Reflection, also known as a flip, mirrors a figure over a specified line called the line of reflection. The image created is a mirror image of the original figure. On a cartesian plane, a line is defined by a linear equation which can be generalized into the format y = mx + c.

Example: Reflecting a letter ‘L’ over the y-axis on a Cartesian plane results in a backward ‘L’. The size and shape of the letter remain unchanged, but its orientation is reversed.
Dilation
Dilation involves resizing a figure by a scale factor relative to a point known as the center of dilation. This transformation changes the size of the figure but retains its shape and orientation. If the scale factor is:
1) Greater than 1 – The shape increases in size
2) Equal to 1 – Retains original size
3) Less than 1 – Shrinks

Example: Dilating a circle with a scale factor of 2 increases the radius of the circle by twice its original length, enlarging the circle while maintaining its shape.
Combinations of Transformations
In practical scenarios, it is important to perform a combination of transformations to the image. The order in which a combination of transformations is applied is crucial, as different sequences can result in different outcomes.
The following diagrams demonstrate the effect of applying two different transformations to a triangle. On the left, the original triangle is first rotated 60 degrees anticlockwise around point (0,0) and then translated by a vector (-2,6). On the right, the same transformations are applied in the reverse order. The outcome in each case is different.
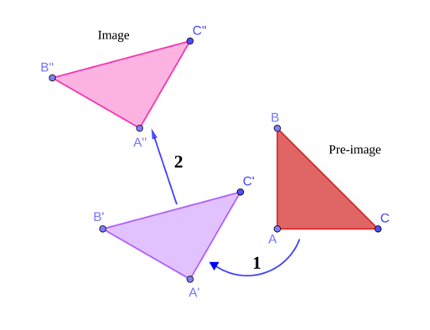
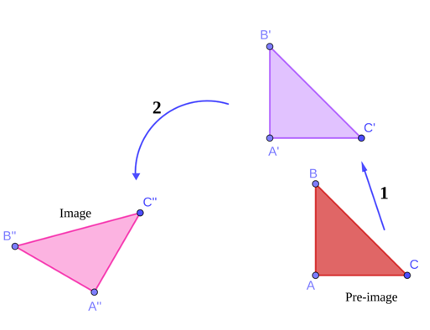
Transformations in Coordinate Geometry
In coordinate geometry, transformations are often represented using algebraic functions. For example, a translation can be represented by adding or subtracting values to the x and y coordinates of a figure’s points. A rotation may involve applying trigonometric functions to these coordinates.
Mathematical Properties of Transformations
Transformations exhibit certain mathematical properties:
Isometry: Some transformations, like translations, rotations, and reflections, are isometries. This means they preserve distances and angles, keeping the original shape and size intact.
Orientation: Reflections change the orientation of a figure (e.g., flipping it over), while translations and rotations do not.
Commutativity: The order of transformations may affect the final result. For instance, translating a figure and then rotating it can yield a different outcome than rotating it first and then translating it.
Geometric Transformations in Real-World Problem Solving
Transformations are not just theoretical concepts; they are applied in real-world problem-solving. For example, in architecture, understanding geometric transformations helps in visualizing and designing structures and their modifications. Architects use transformations to envisage how a building would look from different perspectives or how it would fit into a particular landscape.
Examples of Transformations in Everyday Life
In everyday life, we encounter transformations frequently. For instance, when we see our reflection in a mirror, it’s an example of a reflection transformation. The concept of dilation is observed when using a photocopier to enlarge or reduce a document. Even simple actions like sliding a book across a table (translation) or opening a door (rotation) are practical demonstrations of geometric transformations.
Conclusion
Transformations are a fascinating and essential aspect of mathematics, providing a foundation for understanding and manipulating the geometric world. From artistic design to technological applications, the principles of transformation influence many areas of our lives. Understanding these transformations enhances our appreciation of both the mathematical and the practical world around us. As such, the study of transformations is not only an academic pursuit but also a journey into a world where mathematics meets creativity, innovation, and everyday life.